PFRC inventor Dr. Sam Cohen and his student Taosif Ahsan have published a new journal paper, “An analytical approach to evaluating magnetic-field closure and topological changes in FRC devices,” in Physics of Plasmas (Phys. Plasmas 29, 072507 (2022)). The paper is an Editor’s Pick and has important implications for confining plasma in Field-Reversed Configurations (FRCs).
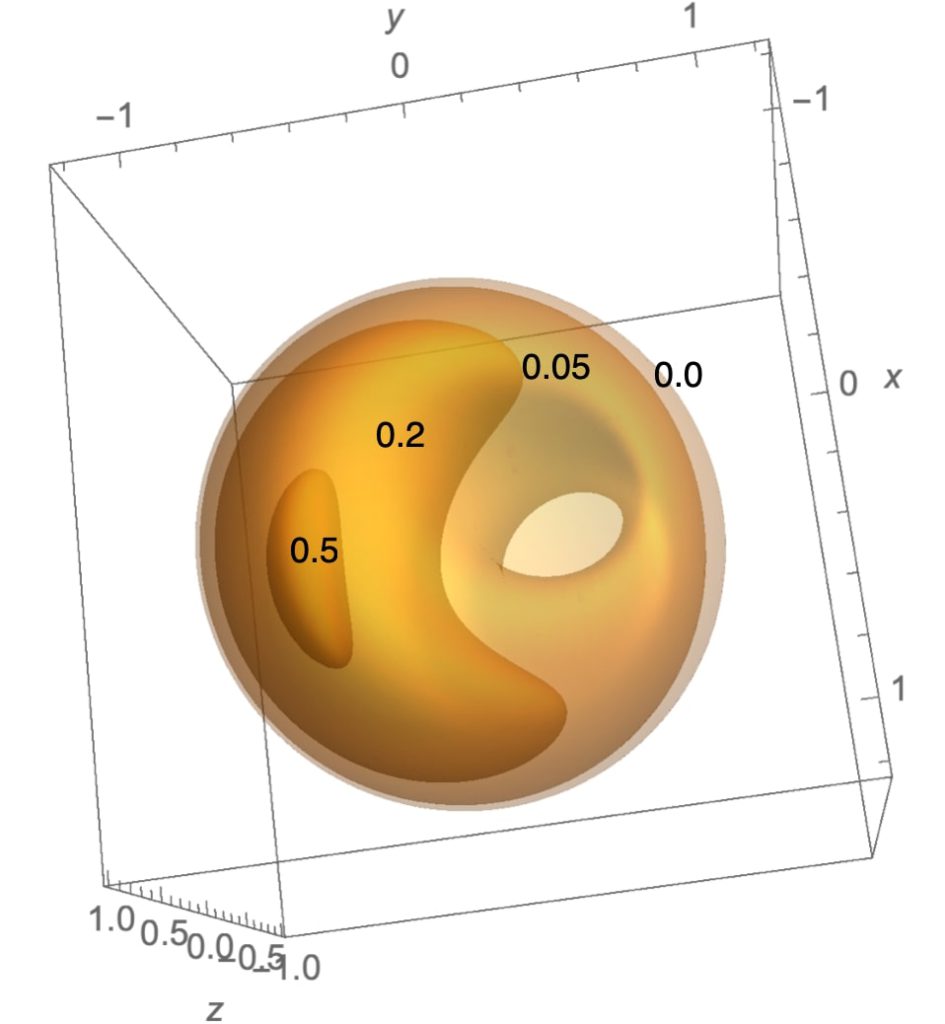
We describe mathematical methods based on optimizing a modified non-linear flux function (MFF) to evaluate whether odd-parity perturbations affect the local closure of magnetic field lines in field-reversed configurations. Using the MFF methodology, quantitative formulas are derived that provide the shift of the field minimum and the threshold for field-line opening, a discontinuous change in field topology.
Paper Abstract
This paper follows up on a 2000 paper by Cohen and Milroy, which made qualitative assertions about changes in magnetic field topology, e.g., movement of the center of separatrix, separator line, and other geometric parameters. Ahsan and Cohen developed the modified flux function (MFF) mathematical tool to quantitatively understand the effects of perturbations on a Solov’ev FRC field structure. The analytical results from this function have reproduced the previous numerical observation that small odd-parity perturbation preserves FRC field structure. In particular, the contours around the equilibrium stay closed.
Closure of magnetic field lines limits plasma losses that would occur due to charged particles leaving the FRC by traveling along open field lines. The paper points out that in a reactor-scale FRC where ions have a large gyroradius relative to the field structure, but electrons have a small radius and follow the field lines, particle and energy losses on the open field lines outside the FRC will be significant. Hence, ensuring closure of field lines is a crucial step toward improved plasma confinement in FRCs.